| Autor |
UgiÄcie belki o zmiennym przekroju |
adi
UÅžytkownik
PostÃģw: 3
Data rejestracji: 28.01.10 |
| Dodane dnia 01/28/2010 16:16 |
|
|
Witam wszystkich forumowiczÃģw! Od jakiegoÅ czasu borykam siÄ z problemem wyznaczenia przekroju belki, ktÃģrego wysokoÅÄ jest zmienna. Jestem stolarzem i nie mam odpowiedniej wiedzy teoretycznej by wiedzieÄ w jakim kierunku ruszyÄ z poszukiwaniami - tu mam nadziejÄ na pomoc kolegÃģw.
WiÄc do rzeczy!
Belka o przekroju prostokÄ
tnym(o zmiennej wysokoÅci) dociskana jest, dwiema siÅami na koÅcach belki, do podÅoÅža. Jak znaleÅšÄ przekrÃģj (krzywÄ
spodu belki, zakÅadajÄ
c gÃģrnÄ
krawÄdÅš jako prostÄ
), ktÃģry spowoduje rÃģwnomierne rozÅoÅženie ciÅnienia na caÅej dÅugoÅci belki?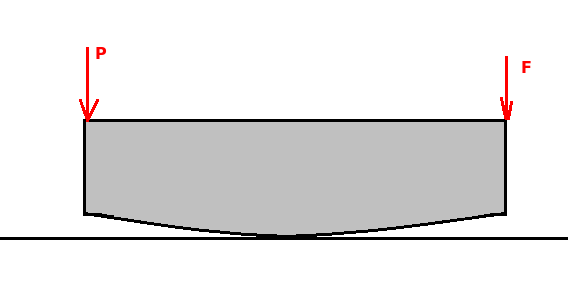
Jak dotÄ
d poradziÅem sobie w praktyce stosujÄ
c belkÄ o prostym przekroju, zdystansowanÄ
do podÅoÅža krzywÄ
, obliczonÄ
z ugiÄcia belki rÃģwnomiernie obciÄ
Åžonej. To rozwiÄ
zanie ma jednak doÅÄ istotne dla mnie wady.
Czy ten zmienny przekrÃģj moÅžna policzyÄ w jakimÅ programie (moÅže byÄ nawet od du.. strony, czyli podajÄ
c krzywÄ
i sprawdzajÄ
c jak rozÅoÅžy ciÅnienie), jeÅželi tak to w jakim (dobrze by byÅo na Linuksa)? Teoria jednak rÃģwnieÅž jest ciekawa i jeÅli ma ktoÅ z was siÅy, by mi wskazaÄ drogÄ do rozwiÄ
zania, to zapraszam do dyskusji.
Pozdrawiam!
Adam
Edytowane przez adi dnia 01/28/2010 16:20 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 01/28/2010 19:18 |
|
|
|
Znaczy trochÄ nie rozumiem, potrzebujÄ wyjaÅnieÅ. Czy chodzi Ci o takÄ
sytuacjÄ, Åže pod obciÄ
Åženiem(jak na rysunku) belka rÃģwnomiernie bÄdzie dociskana do podÅoÅža, tzn w kaÅždym punkcie kontaktu pomiÄdzy belkÄ
i podÅoÅžem bÄdzie taki sam nacisk powierzchniowy? |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
ADMIN
Administrator
PostÃģw: 651
MiejscowoÅÄ: Warszawa, PL
Data rejestracji: 18.10.07 |
| Dodane dnia 01/28/2010 23:18 |
|
|
Chyba tak Piotr, o to wÅaÅnie chodzi ADI-emu (tak to zrozumiaÅem).
Pozdrawiam,
Admin
We live in an age when pizza gets to your home faster than police or an ambulance |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
adi
UÅžytkownik
PostÃģw: 3
Data rejestracji: 28.01.10 |
| Dodane dnia 01/29/2010 07:17 |
|
|
DokÅadnie tak. Dodam jeszcze, Åže nacisk ten moÅže siÄ rÃģÅžniÄ na dÅugoÅci w przedziale powiedzmy 10-15%. Docelowo jest to Åciski stolarski eliminujÄ
cy np. stosowanie na dÅugoÅci metra 8 sztuk ÅciskÃģw tradycyjnych.
Dotychczasowa wersja w czasie pracy (doklejanie " noska" do stopnia):

Edytowane przez adi dnia 01/29/2010 08:19 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 01/29/2010 12:19 |
|
|
Hm to bardzo ciekawy temat, ale trochÄ wymaga czasu na zastanowienie. Tak na szybko powiem, Åže sÄ
dzÄ,Åže to bÄdzie belka winklerowska tylko taka, w ktÃģrej w miejsce sprÄÅžystoÅci podÅoÅža wprowadzamy warunek staÅoÅci siÅy oddziaÅywania. Ale to maÅo, potrzebny by jeszcze byÅ warunek by linia ugiÄcia belki byÅa rÃģwna odwrÃģconej krzywej charakteryzujÄ
cej ksztaÅt belki nieobciÄ
Åžonej. To wszystko mocno komplikuje sprawÄ... MoÅže Åatwiej by byÅo gdyby ta belka byÅa symetryczna...czyli nie byÅa de facto belkÄ
zakrzywionÄ
!
Mam jeszcze jednÄ
wÄ
tpliwoÅÄ: po co Ci ta pÅaska powierzchnia? |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
adi
UÅžytkownik
PostÃģw: 3
Data rejestracji: 28.01.10 |
| Dodane dnia 01/29/2010 18:23 |
|
|
Ta pÅaska powierzchnia to gÃģra belki? JeÅželi tak to jedyny problem z np. wypukÅÄ
powierzchniÄ
widzÄ taki, iÅž materiaÅ to drewno i jako kompozyt wÅÃģknisty mogÅo by pÄkaÄ wzdÅuÅžnie przy rozciÄ
ganiu tak wyciÄtego Åuku.
Walka z Winklerem zapowiada siÄ ciekawie  . Mnie natomiast oÅwieciÅo(albo i nie) takim rysunkiem (tak poglÄ
dowo, pÃģÅ belki): . Mnie natomiast oÅwieciÅo(albo i nie) takim rysunkiem (tak poglÄ
dowo, pÃģÅ belki):
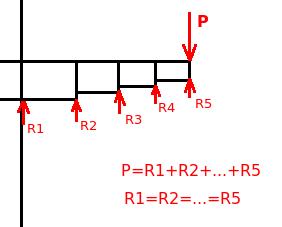
Gdyby naszÄ
belkÄ, upraszajÄ
c, rozbiÄ na krÃģtsze, proste belki i zgiÄ
Ä to do podÅoÅža. SiÅy sÄ
znane, ugiÄcia rÃģwnieÅž, tylko obliczyÄ przekroje 
Edytowane przez adi dnia 01/29/2010 18:24 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 01/31/2010 18:26 |
|
|
To co proponuje Adi atrakcyjnie wyglÄ
da, ale moim zdaniem jest to trudne. OtÃģÅž dlaczego:
jak wiadomo rÃģwnanie ugiÄcia belki moÅžna przedstawiÄ np tak:
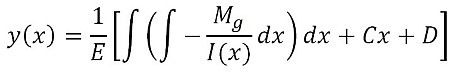
JeÅželi zadanie postawimy tak, Åže szukamy takiego ksztaÅtu belki ktÃģre pod obciÄ
Åženiem ciÄ
gÅym q=const (staÅy doscisk) powoduje ugiÄcie belki dokÅadnie odwrotne do ksztaÅtu belki (wtedy brzeg belki bÄdzie liniÄ
prostÄ
) to jak z rÃģwnania wynika czÅon Mg/I musi byÄ staÅÄ
czyli moment bezwÅadnoÅci musi siÄ zmieniaÄ dokÅadnie wg krzywej zmiany momentu gnÄ
cego a to jest nie tyle niemoÅžliwe co trudne w wykonaniu! Bo w naszej belce moment gnÄ
cy wyraÅža siÄ wzorem 0.5qx(l-x) gdzie l to dÅugoÅÄ belki a wtedy moment bezwÅadnoÅci to a(x) (qx(l-x))^3 czyli aby to byÅo moÅžliwe a(x) czyli szerokoÅÄ belki musiaÅaby siÄ zmieniaÄ wg bardzo fikuÅnej krzywej.... Ale gdyby to pociÄ
gnÄ
Ä dalej to przynajmniej mielibyÅmy rozwiÄ
zanie. Nie mam w tej chwili czasu,ale moÅže ktoÅ to pociÄ
gnie dalej...
Edytowane przez piotr dnia 01/31/2010 18:42 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/02/2010 18:47 |
|
|
Wprowadzic dodatkowe zalozenia warto:
- podloze Winklera,
- dla niewazkiej belki (chyba rowniez dla wazkiej, ale symetrycznej wzdluz plaszczyzny przechodzacej przez srodek rozpietosci) obie sily obciazajace musza byc rowne jesli odpor ma byc rowny (warunek rownowagi wzgledem dowolnego punktu)
Postaram sie wieczorem podac rozwiazanie... |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/02/2010 20:04 |
|
|
Ok, dziecie umyte wiec jest chwilka.
Pare slow komentarza. Rozwiazuje belke obciazajac ja rownomiernym obciazeniem, przez ktore rozumiem odpor. Zakladam, ze obie sily sa takie same, ciezar wlasny zaniedbuje.
Korzystam z rownania osi odksztalconej belki. Zapewne jest to dobre tylko w przypadku, gdy mowimy o belkach doznajacych malych przemieszczen koncow (pominieta geometryczna nieliniowosc, wazne zalozenie Bernoulliego).
Rozwiazanie przeprowadzone w Mathematice, dla kwadratowo zmiennej sztywnosci (mozna oczywiscie dowolnie, ale musialem cos przyjac).
Plik pdf mozna znalezc pod adresem:
http://sawinski.us/downloads/inne/belka_feazone.pdf
Moga byc jakies bledy, wiec raczej jest to wstep do dyskusji
Edit: Pominiety oczywiscie modul Younga...
Edytowane przez sawinski dnia 02/02/2010 20:06 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 02/02/2010 21:18 |
|
|
PrzydaÅoby siÄ jeszcze parÄ sÅÃģw komentarza, albo przynajmniej wykaz oznaczeÅ bo nie widzÄ tego obciÄ
Åženia ciÄ
gÅego... gdzie teÅž jest konieczny warunek Åže siÅa na koÅcach rÃģwna jest sile docisku. RÃģwnanie wydaje mi siÄ rÃģwnaniem II stopnia, a wiÄc powinien byÄ moment gnÄ
cy... nie, jednak poproszÄ o 2,3 sÅowa wyjaÅnienia.
|
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/02/2010 21:51 |
|
|
Oznaczenia:
EI[x] - kwadratowa funkcja sztywnosci (na chybil trafil cos przyjalem)
EI1 - sztywnosc na poczatku i koncu belki,
EI2 - sztywnosc w srodku rozpietosci
w[x] - przemieszczenie,
T[x] - sila tnaca,
l - rozpietosc (mozna spokojnie sie przyczepic, gdyz nie uwzglednia geometrycznej nieliniowosci - belka odksztalcona i 'plaska' sa takiej samej dlugosci)
Rozwiazane rownanie rozniczkowe IV rzedu (II rzedu gdyby EI bylo stale) z warunkami (po kolei jak w zamieszczonym pliku):
- przemieszczenie poczatku belki rowne 0,
- przemieszczenie konca belki rowne 0,
- moment (kat obrotu dokladnie) na poczatku rowny 0,
- kat obrotu na koncu rowny 0
Rozwiazuje belke o nieznanym ksztalcie. Postuluje aby pod wplywem obciazenia rownomiernego (odporu, o wartosci 2P/l) belka ta byla 'plaska'. Uklad wspolrzednych zaczepiam myslowo na krancu belki, stad tez ich przemieszczenia beda 0 (w takim ukladzie, przy takim obciazeniu) - odwrocone zadanie z 1 postu.
Wartosci sil tnacych sa rowne prztylozonym silom - patrz poprawiony pdf.
edit: zamiast 'plaska' pojawial sie jakis usmieszek
Edytowane przez sawinski dnia 02/02/2010 21:54 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
ADMIN
Administrator
PostÃģw: 651
MiejscowoÅÄ: Warszawa, PL
Data rejestracji: 18.10.07 |
| Dodane dnia 02/02/2010 22:27 |
|
|
Ciekawe rozwiÄ
zanie. W wolnym czasie przeanalizuje je sobie...
edit: zamiast 'plaska' pojawial sie jakis usmieszek
Tak, proszÄ przy postowaniu najlepiej zahaczyÄ opcjÄ "WyÅÄ
cz UÅmieszki".
Pozdrawiam,
Admin
We live in an age when pizza gets to your home faster than police or an ambulance
Edytowane przez ADMIN dnia 02/02/2010 22:27 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 02/02/2010 23:16 |
|
|
DziÄkujÄ!
Faktycznie to rÃģwnanie IV rzÄdu (to te dwÃģjki, mathematicÄ
zajmowaÅem siÄ parÄ lat temu). I dalej jestem Ålepy bo w pdf nie potrafiÄ znaleÅšÄ w ktÃģrym miejscu:
Postuluje aby pod wpÅywem obciÄ
Åženia rÃģwnomiernego (odporu, o wartoÅci 2P/l) belka ta byla ' plaska'.
PiszÄ to, bo na razie z moich rozwaÅžaÅ wyszÅo mi, Åže bez winklera to jest nierozwiÄ
zywalne. WiÄc, ktÃģryÅ z nas siÄ pomyliÅ. AbyÅ mÃģgÅ sprawdziÄ co wymyÅliÅem zajrzyj http://feazone.org/downloads/belka.pdf
OczywiÅcie zrobiÅem parÄ zaÅoÅžeÅ, ktÃģre byÄ moÅže sÄ
bÅÄdne, ale w tej chwili, tego nie widzÄ. POMOCY!!!
Edytowane przez piotr dnia 02/02/2010 23:18 |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/03/2010 05:28 |
|
|
|
I dalej jestem Ålepy bo w pdf nie potrafiÄ znaleÅšÄ w ktÃģrym miejscu:...
roz=DSolve[{D[EI[x]*D[w[x], {x, 2}], {x, 2}] == 2 P/l (...) |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/03/2010 06:34 |
|
|
@piotr
jesli mozesz napisz prosze troszke wiecej slow o wzorze 2 i 3, gdyz przy danych oznaczeniach wyglada na to, ze:
- ze wzoru 2 znajac h(x) belki znamy jej przemieszczenia. Czy jezeli zaloze sobie h(x) znane to ten wzor jest prawdziwy i spelnia rownanie osi odksztalconej?
- ze wzoru 3: postulujesz zeby stosunek ten byl staly, ale co ze swobodnymi koncami, gdzie M rowne 0?
Jesli jakas uwaga jest tak oczywista, ze nie ma sensu tlumaczyc, to napisz 'debil' a ja sie temu przyjrze moze wieczorem |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 02/03/2010 08:10 |
|
|
Faktycznie, na koÅcach mam nieoznaczonoÅÄ... ZresztÄ
cho*ra tak to jest jak zamiast wziÄ
Ä oÅÃģwek, od razu siÄ pisze na gotowo, przecieÅž mam skopany wzÃģr 4 uh, muszÄ do tego siÄ
ÅÄ zamiast pisaÄ z doskoku, moÅže dzisiaj wieczorem....
czy ten wzÃģr ktÃģry napisaÅeÅ czyta siÄ tak:
d^2/dx^2(EI(x) d^2/dx^2(w(x)))=q
???
jeÅželi tak, to z czego wynika pÅaskoÅÄ belki, a jeÅželi nie, to jak to czytaÄ? |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/03/2010 16:11 |
|
|
Ajajaj, rzeczywiscie
Warunki nie sa oczywiscie na katy obrotu, bo na druga pochodna, czyli momenty. Obciazona belka jest na poczatku plaska, a pod wplywem odporu przyjmuje ksztalt opisany u mnie w[x]. A wiec sytuacja bedzie nastepujaca:
- gdy belke o wyliczonym ksztalcie obciaze teraz odporem, to powinna ona byc plaska czyli gdy pisalem: czyli gdy pisalem:
Rozwiazuje belke o nieznanym ksztalcie. Postuluje aby pod wplywem obciazenia rownomiernego (odporu, o wartosci 2P/l) belka ta byla '  laska'. Uklad wspolrzednych zaczepiam myslowo na krancu belki, stad tez ich przemieszczenia beda 0 (w takim ukladzie, przy takim obciazeniu) - odwrocone zadanie z 1 postu. 
Lecz coby byc szczerym, rownanie osi odksztalconej (tak, takie jak piotr napisal, czyli (EI(x)w''(x))''=q uczy sie na drugim roku studiow), czyli wiekszosc studentow powinna to rozwiazac szybciej niz my
Widze rowniez pewne wady w swoim rozwiazniu, ale nie sadze, zeby mialy wiekszy wplyw na wynik (relacja zalozona sztywnosc, a otrzymany ksztalt). Rowniez male niesymetrie powinny sie miescic w bledzie ktory autor zalozyl, czyli ~15%. Stad wydaje mi sie, ze techniczny problem jest rozwiazany, natomiast naukowy chyba wciaz jeszcze nie. |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/03/2010 16:17 |
|
|
Jeszcze jedna krotka uwaga, strona prof. Brzakaly:
http://www.ib.pwr.wroc.pl/brzakala/uzupelnienia/w2.pdf (kilka razy naciskalem odswiez nim sie otworzylo). Jest opisany na oko podobny przypadek, ale zerkalem na to moze 20 sekund. Metoda Bleicha - pewnie nawet na studiach nia liczylem cos, ale przyznam sie ze juz nie pamietam (a mialem z prof. Brzakala) |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
piotr
Super Administrator
PostÃģw: 1432
Data rejestracji: 17.05.07 |
| Dodane dnia 02/03/2010 19:18 |
|
|
No pdf poprawiony (wstydliwy byk zniknÄ
Å jak kamfora).Na szczÄÅcie nie zmieniÅ on moich wnioskÃģw. Ta nieciÄ
gÅoÅÄ jest (i owszem) ale lewostronna pochodna zmierza do wÅaÅciwej wartoÅci, tak wiÄc abstrahujÄ
c od rozwaÅžaÅ teoretycznych, praktycznie nie miaÅoby to znaczenia.
NajwaÅžniejszym zaÅoÅženiem, ktÃģre, dostrzegam to teraz, muszÄ jednak udowodniÄ jest staÅoÅÄ stosunku momentu gnÄ
cego i bezwÅadnoÅci przekroju... no cÃģÅž zobaczymy...
Co do Twojego rozwiÄ
zania...
Po pierwsze dziÄkujÄ za wyjaÅnienia, nie rozumieliÅmy siÄ, bo myÅlÄ
c o ksztaÅcie belki miaÅem na myÅli zmiennoÅÄ jej przekroju. Ty zaÅ postulujesz wprowadziÄ belkÄ wstÄpnie wygiÄtÄ
tak, wiÄc byÅoby to rozwiÄ
zanie bardziej zbliÅžone do tego co proponuje ADI.
Mam tylko jednÄ
zagwozdkÄ: czy rzeczywiÅcie uzyskasz tÄ siÅÄ odporu na dociskanym przedmiocie. No bo zauwaÅž, Åže proces dochodzenia do caÅego obciÄ
Åženia jest nieliniowy(ze wzglÄdu na powiÄkszajÄ
cÄ
siÄ strefÄ kontaktu w trakcie dociskania). WziÄ
Åem sobie kawaÅek wygiÄtej belki (taki dziecinny Åuk) i dociskaÅem do biurka, okazuje siÄ, Åže zrobiÅa mi siÄ dziura na jej Årodku (brak docisku). OczywiÅcie ksztaÅt Åuku nie byÅ zgodny z Twoim rÃģwnaniem ale... No wÅaÅnie ale... problem jest w tym obciÄ
Åženiu ciÄ
gÅym! Proces teoretycznie (z zaÅoÅžonÄ
dokÅadnoÅciÄ
) da siÄ odwrÃģciÄ ale jak go praktycznie zrealizowaÄ... MyÅlÄ, Åže bez podÅoÅža Winklera ani rusz... |
|
|
| Autor |
RE: UgiÄcie belki o zmiennym przekroju |
sawinski
UÅžytkownik
PostÃģw: 29
Data rejestracji: 02.02.10 |
| Dodane dnia 02/03/2010 19:30 |
|
|
|
Podloze Winklera jest jednym z postulatow wprowadzonych na poczatku. Dla polrzestrzeni sprezystej nie da sie osiagnac rozwiazania w zakresie jednakowego odporu na dlugosci. |
|
|

