Elementy analizy modelu felgi z uÅŒyciem Komputerowej Dynamiki PÅynów Komputerowa Dynamika PÅynów (ang. Computational Fluid Dynamics CFD) to jedna z dziedzin mechaniki pÅynów, zajmujÄ
ca siÄ rozwiÄ
zywaniem i analizÄ
problemów przepÅywów masy i ciepÅa, z pomocÄ
metod numerycznych. Zagadnienie to, którego rozwój zwiÄ
zany jest z pracÄ
wielkich matematyków XIX wieku znane jest dziÅ czÄsto pod niezbyt ÅcisÅÄ
nazwÄ
„rozwiÄ
zywania ukÅadu równaÅ Naviera – Stokesa”. Pomimo silnych teoretycznych inklinacji problemu, wielki rozwój metod CFD w ciÄ
gu ostatniego ÄwierÄwiecza zaowocowaÅ moÅŒliwoÅciÄ
ich inÅŒynierskiego zastosowania w projektowaniu i analizie systemów inÅŒynierskich przy redukcji kosztów i czasu rozwoju produktu. Celem tego artykuÅu nie jest próba wyjaÅnienia teoretycznych podstaw mechaniki pÅynów, nie moÅŒe byÄ równieÅŒ postrzegany jako opis testowania implementacji numerycznej ani wybranego kodu. Celem autora jest przedstawienie podstawowych zastosowaÅ CFD oraz przybliÅŒenie jak najszerszemu krÄgowi uÅŒytkowników i entuzjastów metod numerycznych tej jeszcze nieczÄsto uÅŒywanej techniki. DziÄki uprzejmoÅci organizatorów serwisu feazone.org moÅŒliwe byÅo uÅŒycie rozwaÅŒanego szerzej modelu felgi, którego obliczenia wytrzymaÅoÅciowe mogÄ
w interesujÄ
cy sposób uzupeÅniÄ siÄ z podejÅciem CFD; z pewnoÅciÄ
zaowocuje to szerszym spojrzeniem na kwestiÄ projektowania wyrobu koÅcowego. Cel pracy W niniejszej pracy przestawiono obliczenia przepÅywu medium gazowego (powietrze) wokóŠmodelu felgi samochodowej z dorysowanÄ
schematycznie oponÄ
. Celem byÅa wizualizacja opÅywu wokóŠprzedmiotu, zbadanie siÅ aerodynamicznych dziaÅajÄ
cych na fragment domeny obliczeniowej oraz pobieÅŒna analiza efektów w warstwie przyÅciennej. Przede wszystkim jednak chodziÅo o demonstracjÄ podstawowych aspektów problematyki obliczeÅ CFD. Geometria i siatka W niniejszej pracy obiektem badanym jest przeskalowany model felgi samochodowej o Årednicy rzÄdu 100 mm („felga prosta”). Model ten poddano uproszczeniom geometrycznym polegajÄ
cym na zapeÅnieniu otworu na piastÄ, otworów na Åruby mocujÄ
ce oraz otworów na Åruby spinajÄ
ce czÄÅci felgi. Dorysowana zostaÅa opona o arbitralnie przyjÄtym zarysie; bieÅŒnik potraktowano jako ÅcianÄ
szorstkÄ
o szorstkoÅci rzÄdu 0.2 mm. Domena obliczeniowa (Rysunek 1) ma wymiary 200 x 250 x 700 mm, badany model umieszczony jest w przedniej czÄÅci. Model koÅa nie obraca siÄ, natomiast zaÅoÅŒono celowy odstÄp pomiÄdzy spodniÄ
czÄÅciÄ
opony a podÅoÅŒem (rzÄdu 1mm) – jego znaczenie zostanie opisane dalej. Siatki elementów skoÅczonych liczÄ
okoÅo 3,8 mln elementów o wymiarze maksymalnym 6 mm. Siatki skÅadajÄ
siÄ z elementów czworobocznych, z istotnym udziaÅem pryzmatycznych elementów dla warstwy przyÅciennej. Badania modelu wykonano dla prÄdkoÅci przepÅywu V równej 20 m*s-1, 40 m*s-1oraz 60 m*s-1; przyjmujÄ
c jako medium powietrze o lepkoÅci μ liczba Reynoldsa ReL modelu rzÄdu 250 mm kolejno okoÅo 300000, 600000 i 900000. KorzystajÄ
c z zaleÅŒnoÅci: wynosiÅa dla rozmiaru charakterystycznego 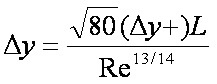 (1) (1)
Gdzie Δy – odlegÅoÅÄ pierwszego wÄzÅa siatki od powierzchni modelu [m]: Δy+ – bezwymiarowa odlegÅoÅÄ pierwszego wÄzÅa siatki od powierzchni modelu. MoÅŒna podaÄ warunki tworzenia siatki dla oczekiwanych wartoÅci Re. Zgodnie z zaleceniami wiÄkszoÅci modeli „high-Re” turbulencji Δy+ powinna wynosiÄ okoÅo 10. W zwiÄ
zku z tym, odlegÅoÅÄ pierwszego wÄzÅa siatki od powierzchni dla wymienionych liczb Re wynosiÅa zgodnie z równaniem 1 od 0.2 mm do 0.07 mm. Siatka warstwy przyÅciennej pokrywa caÅy model koÅa wraz z podÅoÅŒem (Rysunek 2), majÄ
c 10 warstw. GruboÅÄ warstw liczÄ
c od powierzchni wzrasta co kaÅŒdÄ
o 10%. Opisane siatki zostaÅy wybrane po badaniach na siatkach dwukrotnie liczniejszych i o poÅowÄ mniej licznych. PoniewaÅŒ istotne parametry przepÅywu zmieniaÅy siÄ o okoÅo 3% wybrano wariant poÅredni jako kompromis dokÅadnoÅci i czasu obliczeÅ. 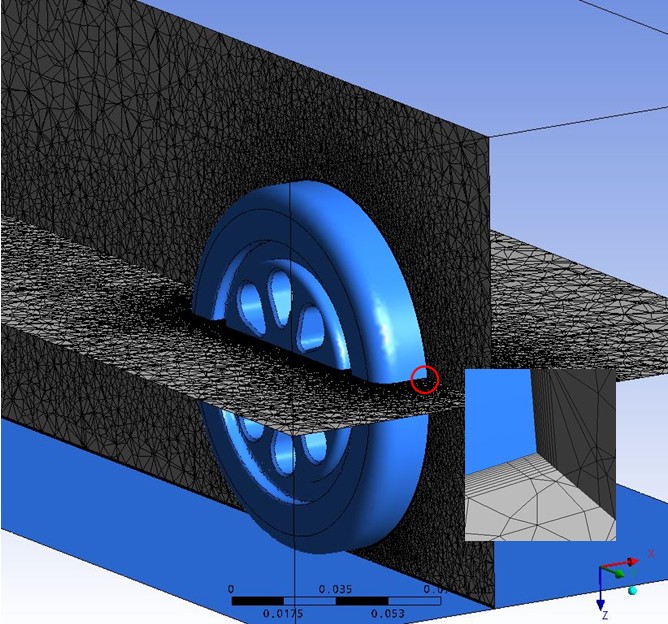
Rysunek 1 i Rysunek 2 (inset). Widok ogólny fragmentu domeny obliczeniowej – zwraca uwagÄ zagÄszczenie siatki wokóŠmodelu. Po prawej stronie detal powierzchni opony ukazujÄ
cy siatkÄ warstwy przyÅciennej. Obliczenia Opisywany model badany byÅ w adiabatycznym przepÅywie powietrza o temperaturze 200C, w reÅŒimie turbulentnym, za pomocÄ
modelu k-e o standardowych parametrach. Wykonano nastÄpujÄ
ce obliczenia: - Dla prÄdkoÅci napÅywu powietrza V 20m*s-1, 40m*s-1oraz 60m*s-1 na osobno przygotowanych siatkach, celem zbadania siÅ dziaÅajÄ
cych na powierzchniÄ czoÅowÄ
opony,
- Dla prÄdkoÅci napÅywu powietrza V 20m*s-1 przy uÅŒyciu siatek dla wyÅŒszych liczb Re dla zbadania wpÅywu zmieniajÄ
cej siÄ wartoÅci Δy+ na naprÄÅŒenia (ang. shear stress rate) przy powierzchni opony w osi modelu
Wszystkie obliczenia wykonano dla zbieÅŒnoÅci numerycznej poniÅŒej 10-4, imbalancje wszystkich równaÅ byÅy kaÅŒdorazowo niÅŒsze niÅŒ 0.5%. Czas kaÅŒdego obliczenia wyniósÅ okoÅo 1 godziny. Wyniki i dyskusja Linie przepÅywu powietrza o prÄdkoÅci poczÄ
tkowej 20 m*s-1 wokóŠmodelu, leÅŒÄ
ce w pÅaszczyznach prostopadÅych przedstawiono na rysunku 3; wlot znajduje siÄ po stronie prawej rysunku. Widoczne jest sprÄÅŒanie strug wzdÅuÅŒ profilu opony oraz w naroÅŒniku opony pomimo zaokrÄ
glenia. DziÄki duÅŒej energii kinetycznej warstwy przyÅciennej nie dochodzi do wyraźnego oderwania strugi za oponÄ
. Widoczne sÄ
równieÅŒ strugi powietrza „wpychane” pod koÅo. PoniewaÅŒ w odlegÅoÅÄ pomiÄdzy dolnÄ
czÄÅciÄ
opony a podstawÄ
domeny obliczeniowej jest mniejsza niÅŒ gruboÅÄ warstwy przyÅciennej powietrze jest po dotarciu tam silnie wypychane na zewnÄ
trz. Strugi te nie sÄ
wiÄc widoczne na wizualizacji w ich pÅaszczyźnie poczÄ
tkowej. 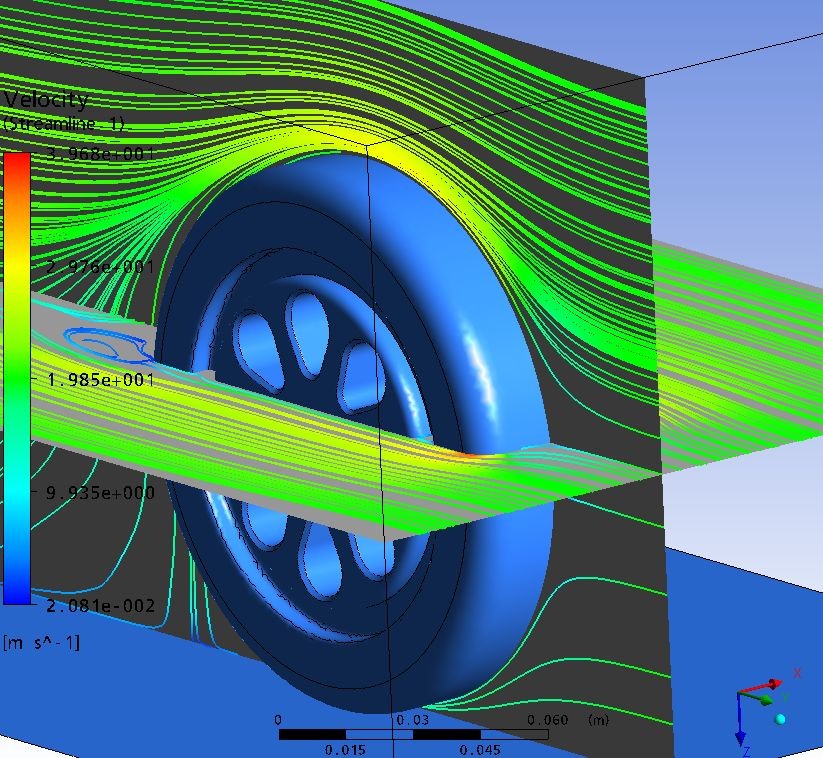
Rysunek 3. Linie prÄ
du wokóŠmodelu, prÄdkoÅÄ 20 m*s-1. 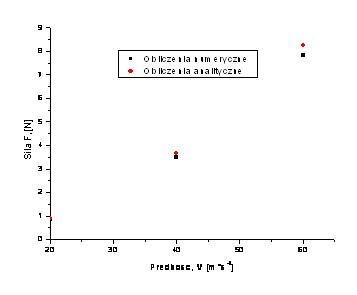
Rysunek 4. SiÅa oporu aerodynamicznego wywierana przez przepÅywajÄ
ce powietrze na tocznÄ
powierzchniÄ (bieÅŒnik) opony. Rysunek 4 przedstawia wyniki obliczeÅ siÅ oporu aerodynamicznego dziaÅajÄ
cych na powierzchniÄ bieÅŒnika opony. Punkty czarne prezentujÄ
obliczenia numeryczne. Punkty czerwone obrazujÄ
wyniki obliczeÅ siÅy oporu F bryÅy o wspóÅczynniku oporu Cx zgodnie ze wzorem: 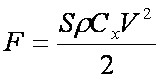 (2) (2)
Gdzie: S – powierzchnia czoÅowa bryÅy [m2], ρ – gÄstoÅÄ medium [kg*m-3]. Dla podanych wymiarów koÅa przyjÄto wspóÅczynnik oporu Cx równy 0.5. Widoczna jest zgodnoÅÄ obliczeÅ numerycznych i analitycznych, przy czym opór wyliczony analitycznie ma wartoÅÄ wyÅŒszÄ
o 5% do 7% w caÅym zakresie prÄdkoÅci. PrawdopodobnÄ
przyczynÄ
jest zaokrÄ
glenie brzegów opony co moÅŒe obniÅŒaÄ wspóÅczynnik Cx jednak wartoÅÄ taka nie jest autorowi znana. WaÅŒnym zagadnieniem w obliczeniach konstrukcji oddziaÅujÄ
cych z medium pÅynnym jest analiza zjawisk zachodzÄ
cych w warstwie przyÅciennej. W opisywanym projekcie badania naprÄÅŒeÅ w pÅynie w najwiÄkszej bliskoÅci omywanych powierzchni polegaÅy na okreÅleniu zaleÅŒnoÅci wartoÅci sumy skÅadowych tensora naprÄÅŒeÅ przy prÄdkoÅci przepÅywu 20m*s-1Re. Z powodu sÅabej nieliniowoÅci mianownika w równaniu (1) moÅŒna zaÅoÅŒyÄ, ÅŒe podwojenie liczby Re owocuje dwukrotnym zmniejszeniem odlegÅoÅci pierwszego wÄzÅa siatki (w którym wyliczane sÄ
naprÄÅŒenia) od powierzchni, czyli jest równowaÅŒne zmniejszeniu Δy+. Na rysunku 5 zawarto porównanie naprÄÅŒeÅ mierzÄ
c je wzdÅuÅŒ krzywej bÄdÄ
cej przeciÄciem powierzchni opony z pionowÄ
pÅaszczyznÄ
jak na rysunkach 1 i 3. KÄ
t Ф jest kÄ
tem pomiÄdzy normalnÄ
do powierzchni opony a kierunkiem napÅywu powietrza. Wykres ten moÅŒna interpretowaÄ nastÄpujÄ
co: idÄ
c od wspóÅrzÄdnej cosФ=0 po dolnej gaÅÄzi krzywych w lewo podÄ
ÅŒamy od najniÅŒszego punktu koÅa w stronÄ napÅywu. Na wykresie nastÄpuje gwaÅtowny (nieciÄ
gÅy) skok naprÄÅŒeÅ w punkcie, w którym siatka jest juÅŒ zbyt „gruba” i nie przepuszcza strug. PostÄpujÄ
c dalej po obwodzie opony w stronÄ punktu natarcia obserwujemy spadek naprÄÅŒeÅ do niewielkich wartoÅci – naprÄÅŒenie nie spadajÄ
jednak do 0 co byÅoby cechÄ
idealnie wybranego punktu natarcia, krawÄdź tnÄ
ca nie leÅŒy jednak dokÅadnie w osi opony. PostÄpujÄ
c dalej w kierunku najwyÅŒszego punktu na kole mijamy maksimum naprÄÅŒeÅ (na rysunku 3 najwiÄksze sprÄÅŒenie strug) i zmierzamy w stronÄ punktu najbardziej „osÅoniÄtego”. Nie widaÄ jednak gwaÅtownego oderwania strugi. W punkcie o wspóÅrzÄdnej cosФ=-1 (z „tyÅu” opony”) wartoÅÄ naprÄÅŒeÅ pozostaje niezerowa. W sytuacji idealnej symetrii przykÅadu wartoÅÄ naprÄÅŒeÅ w tym punkcie, przewidywana przez model k-e powinna byÄ równa 0 co jest jednÄ
z cech tego modelu. Charakterystycznym pozostaje równieÅŒ fakt, ÅŒe najwiÄksze róŌnice pomiÄdzy wartoÅciami naprÄÅŒeÅ wystÄpujÄ
w miejscach o najwiÄkszych wartoÅciach ciÅnienia (prÄdkoÅciach przepÅywu). Czym bliÅŒej powierzchni znajduje siÄ pierwszy wÄzeÅ siatki tym wiÄksza jest wartoÅÄ gradientu prÄdkoÅci i naprÄÅŒeÅ. Krzywe dla wartoÅci 2.5y+ i 5y+ leÅŒÄ
bliÅŒej siebie, co moÅŒe sugerowaÄ uÅŒycie nieco gÄstszych siatek w warstwie przyÅciennej.
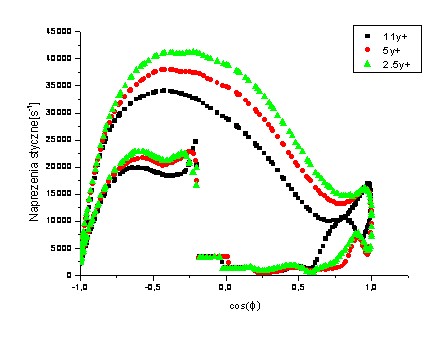 Rysunek 5. WartoÅÄ naprÄÅŒeÅ w pÅynie na powierzchni opony wzdÅuÅŒ linii powstajÄ
cej przez przeciÄcie pÅaszczyzny pionowej z rysunków 1 i 3 z powierzchniÄ
opony. Podsumowanie W pracy niniejszej przedstawiono wybrane elementy obliczeÅ aerodynamicznych modelu felgi wraz z oponÄ
w zakresie prÄdkoÅci powietrza do 60m*s-1, przedstawiono warunki brzegowe i zarys zagadnienia tworzenia siatki obliczeniowej. SiÅa oporu aerodynamicznego wyliczona metodÄ
CFD pozostaje w zgodzie z wynikami analitycznymi na poziomie 5%. Dalsze prace mogÅyby polegaÄ na dodaniu ruchu obrotowego opony, przetestowaniu innych modeli turbulencji (zwÅaszcza w kontekÅcie oderwania strug) lub szerszej analizie juÅŒ otrzymanych wyników. Autor zachÄca do dyskusji nad zagadnieniem obliczeÅ CFD. Åukasz „Luk_Fiz” Czopyk Autor skÅada podziÄkowania organizatorom i spoÅecznoÅci serwisu feazone.org za udostÄpnienie modelu felgi. | 
