BŇāńôdy grube Literatura przedmiotu podaje dwa pojńôcia weryfikacja i walidacja. Ten pierwszy termin odnoszńÖc sińô wŇāaŇõnie do weryfikacji uzyskanego rozwińÖzania (podkreŇõlńô, Ňľe jakieŇõ rozwińÖzanie musi juŇľ byńá) jest nam bliŇľszy. JednakŇľe bŇāńôdy grube, o czym warto pamińôtańá, to bardzo czńôsto jest teŇľ strefa walidacji. Walidacji czyli weryfikacji przyjńôtych zaŇāoŇľeŇĄ. I chońá byńá moŇľe bardziej pasowaŇāby tu termin bŇāńôdy fundamentalne pozostanńô przy moim oznaczeniu i zdefiniujńô bŇāńôdy grube jako te , kt√≥re powodujńÖ generalnńÖ zmianńô uzyskanych wynik√≥w. PozostaŇāe bŇāńôdy, wedle tej klasyfikacji powodujńÖ zaŇõ odstńôpstwa lokalne lub niewielkie wartoŇõciowo (liczńÖc oczywiŇõcie wzglńôdnie). Chońá bŇāńôdy grube naleŇľńÖ do wydawaŇāoby sińô Ňāatwych do znalezienie niestety tak nie jest. PodstawowńÖ przyczynńÖ jest wŇāaŇõnie to, Ňľe zwykle trudny do odszukania (a nawet zorientowania sińô, Ňľe go popeŇāniamy) bŇāńÖd gruby powstaje u samych postaw obliczeŇĄ. WŇāaŇõnie wtedy gdy tworzymy zrńôby naszych obliczeŇĄ: gdy dobieramy model do opisywanych zjawisk, gdy gromadzimy dane dot. modelu, gdy budujemy pierwsze szkice modelowanego zjawiska. Co innego oczywiste bŇāńôdy grube, przyŇāoŇľenie siŇāy 10-krotnie wińôkszej, zmiana staŇāych materiaŇāowych o trzy rzńôdy wielkoŇõci, itp. Przy odrobinie intuicji wyniku zar√≥wno zorientowanie sińô co do bŇāńôdu jak i jego odszukanie nie powinno nastrńôczyńá problem√≥w. W pierwszej czńôŇõci artykuŇāu nazwaŇāem je bŇāńôdami mierzalnymi, ze wzglńôdu na fakt, Ňľe rozpoznajemy je po wartoŇõci uzyskanych parametr√≥w fizykalnych: np. przemieszczeniu lub naprńôŇľeniu maksymalnym . BŇāńôdy mierzalne Aby zrozumieńá bŇāńôdy mierzalne najlepiej pokaŇľńô na przykŇāadach ich wpŇāyw na uzyskiwany wynik. Na pierwszy ogieŇĄ weŇļmy zmiany pewnych parametr√≥w fizycznych (staŇāych fizycznych i geometrycznych ) modelu. Pozwoli to na wyrobienie sobie pewnego wyczucia co do prawidŇāowoŇõci wynik√≥w. Jako przykŇāad weŇļmy referencyjny model dla wielu system√≥w liczńÖcych. Jest to pŇāyta prostokńÖtna prosto podparta opisana przez Timoshenko, S. P. and Woinowsky-Krieger, “Theory of Plates and Shells,” McGraw-Hill Book Co., 2 wydanie z 1962 r. na stronach 120-143. PŇāyta jest wykonana ze stali stopowej o parametrach (w celu por√≥wnania z innymi systemami liczńÖcymi zachowaŇāem oryginalne jednostki anglosaskie): E = 30,000,000 psi =210000 MPa ν= 0.3 h = 1 in = 25,4 mm a = b = 40 in = 1012 mm F = 400 lbf =1779,2888N Ze wzglńôdu na symetrińô zamodelowano ¼ pŇāyty, obcińÖŇľenie przyŇāoŇľono w jej Ňõrodku (wńôzeŇā 25) Problem przedstawiono na poniŇľszym rysunku (rys.1). Uzyskajmy w pierwszym podejŇõciu prawidŇāowe wyniki. 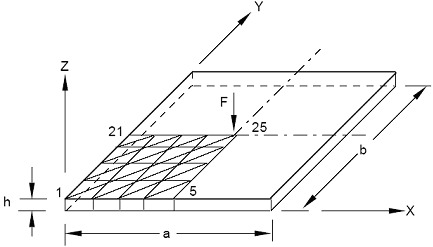
Rys.1 O jakoŇõci rozwińÖzania numerycznego Ňõwiadczy odstńôp od rozwińÖzania teoretycznego, kt√≥re wynosi : 0.0270230 [in] bŇāńÖd wynosi wińôc mniej niŇľ 0.4%. SprawdŇļmy teraz wpŇāyw zmian wŇāasnoŇõci materiaŇāowych na wynik: Opis modelu | Max naprńôŇľenia [psi] | Max przemieszczenie [in] | | Referencyjne MES | 7865.2 | 0,027123 | | 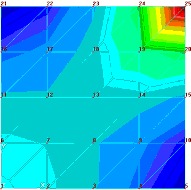
| 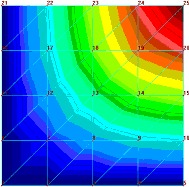
| | h= 1 in=25.mm E= 30,000,000 psi =210000 MPa ν = 0.1 zmniejszamy wsp√≥Ňāczynnik poissona 3 krotnie | 6661.3(zm. 15,3%) | 0,029489(zm. 8,3%) | | 
| 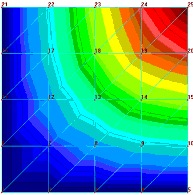
| | h= 1 in=25.mm E=3,000,000 psi =21000 MPa ν =0.3 zmniejszamy moduŇā Younga 10 krotnie | 7851(zm. 0.1%) | 0, 22369(zm. 724%) | | 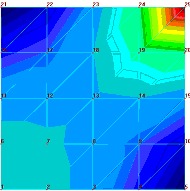
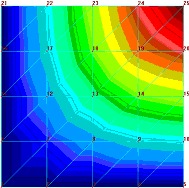
| 
| | h=0.1 in=2.53.mm E= 30,000,000 psi =210000 MPa ν = 0.3 gruboŇõńá pŇāyty zmniejszona 10 krotnie | 785110(zm.9882%) | 27.123(zm. 99900%) | | 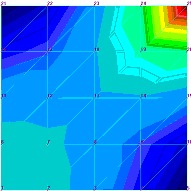
| 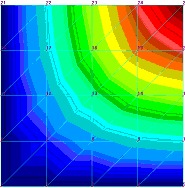
| ZauwaŇľmy na poczńÖtek, Ňľe tylko zmiana wsp√≥Ňāczynnika poissona spowodowaŇāa istotniejszńÖ zmianńô jakoŇõciowńÖ obrazu pola naprńôŇľeŇĄ (chońá w bardziej skomplikowanym modelu trudno tńô zmianńô uznańá za „wykrywalnńÖ”). DokŇāadnie odwrotna sytuacja jest w wynikach iloŇõciowych. Najwińôksza zmiana zaszŇāa w modelu, kt√≥ry w obrazie jakoŇõciowym jest bardzo zbliŇľony do wyniku referencyjnego w modelu z pomyŇākńÖ w gruboŇõci pŇāyty. Co ciekawe obraz jakoŇõciowy pola przemieszczeŇĄ r√≥Ňľni sińô w spos√≥b zauwaŇľalny tylko przy zmianie moduŇāu Younga i gruboŇõci pŇāyty. Zmiana wsp√≥Ňāczynnika poissona nie wywiera zaŇõ istotnego wpŇāywu. CiekawostkńÖ, chońá oczywistńÖ ze wzglńôdu na matematycznńÖ stronńô zagadnienia, jest wpŇāyw zmiany moduŇāu Younga na pole naprńôŇľeŇĄ – a wŇāaŇõciwie jego brak. Jednak czńôsto nie zastanawiamy sińô nad realnymi konsekwencjami zapis√≥w r√≥wnaŇĄ, dlatego warto uzmysŇāowińá sobie to na konkretnym problemie. Jak widańá na podstawie powyŇľszych przykŇāad√≥w istnieje potrzeba znajomoŇõci przybliŇľonej wartoŇõci oczekiwanego wyniku. Bez tej wiedzy bńôdziemy mieli kŇāopoty nie tyle ze znalezieniem bŇāńôdu ile w zorientowaniu sińô, Ňľe go popeŇāniamy. Widańá teŇľ na powyŇľszych przykŇāadach, Ňľe jeŇľeli nie dysponujemy wiarygodnym benchmarkiem naszego zagadnienia, musimy szczeg√≥lnie duŇľo uwagi poŇõwińôcińá weryfikacji danych. BŇāńôdy intuicyjne PodziaŇā bŇāńôd√≥w, kt√≥ry tu proponuje wynika z faktu, Ňľe preferujńô podejŇõcie praktyka. Nie zaleŇľy mi na klasyfikacji bŇāńôd√≥w jako takich ale na usystematyzowaniu podejŇõcia do znajdowania bŇāńôd√≥w w naszych modelach. SkńÖd wińôc nazwa bŇāńôdy intuicyjne? SńÖ to bowiem bŇāńôdy, kt√≥re najczńôŇõciej wyczuwamy w uzyskanych wynikach na podstawie intuicji wyrobionej doŇõwiadczeniem i dopiero tak ”wykryte” bŇāńôdy staramy sińô zdiagnozowańá. OczywiŇõcie, Ňľe weryfikacjńô naleŇľy zawsze przeprowadzańá w oparciu o dostńôpne metody, ale z doŇõwiadczenia teŇľ wiem, Ňľe zazwyczaj wyniki obliczeŇĄ jakkolwiek szybko by nie powstawaŇāy sńÖ i tak sp√≥Ňļnione i presja czasu doprowadza do rezygnacji z czńôŇõci zabieg√≥w weryfikacyjnych (cokolwiek naukowcy na ten temat sńÖdzńÖ). Wr√≥ńámy jednak na poczńÖtek do naszego przykŇāadu. ZaŇā√≥Ňľmy, Ňľe nastńÖpiŇāa pewna pomyŇāka w wińôzach. Uzyskany obraz naprńôŇľeŇĄ i przemieszczeŇĄ przedstawia poniŇľszy rysunek: 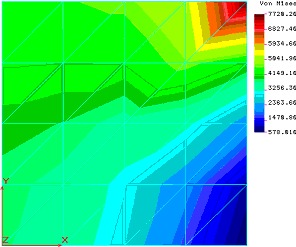 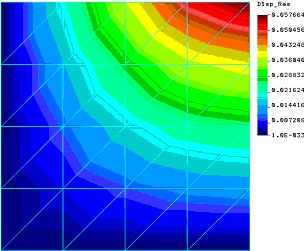
Rys.2 Na kolejnym mamy obraz deformacji pŇāyty na tle pŇāyty nieodksztaŇāconej, pokazano teŇľ punkt przyŇāoŇľenia obcińÖŇľenia: Rys 3. Zanim zaczniemy analizńô przypomnijmy sobie na co zwracańá uwagńô przy pierwszym kontakcie z wynikami o czym m√≥wiliŇõmy w pierwszej czńôŇõci artykuŇāu: a) szukaj ekstrem√≥w (zazwyczaj jesteŇõmy w stanie wskazańá miejsca maksymalnego i minimalnego ugińôcia lub og√≥lnie wystńôpowania pewnej wielkoŇõci wynikowej), b) szukaj logiki (konstrukcja „podńÖŇľa” za obcińÖŇľeniem), c) szukaj „gŇāadkoŇõci” (wszelkie duŇľe skoki wartoŇõci wynikowych muszńÖ mieńá sw√≥j pow√≥d, bńÖdŇļ to w obcińÖŇľeniu bńÖdŇļ to w charakterystyce modelu), d) szukaj niemoŇľliwego (np. .konstrukcja przemieszcza sińô w miejscu gdzie podobnńÖ sńÖ wińôzy). Przeanalizujmy uzyskane wyniki pod kńÖtem tych wskaz√≥wek: Wskaz√≥wka a : Obraz przemieszczeŇĄ nie budzi pod tym wzglńôdem zastrzeŇľeŇĄ – maksima sńÖ w odpowiednim miejscu – punkt przyŇāoŇľenia siŇāy, minima takŇľe – brzeg z odebranymi stopniami translacyjnymi. Obraz naprńôŇľeŇĄ jednak nie jest juŇľ tak poprawny. ZauwaŇľmy, Ňľebrak powodu aby naprńôŇľenia w g√≥rnym lewym fragmencie modelu odbiegaŇāy od tych z prawego dolnego rogu. A skoro brak powodu to naleŇľy to sprawdzińá! Wskaz√≥wka b : Konstrukcja zachowuje sińô logicznie odksztaŇācenia zachodzńÖ r√≥wnomiernie w kierunku zadanego obcińÖŇľenia. Wskaz√≥wka c : Tu w zasadzie jest tylko jeden punkt zaczepienia. W obrazie naprńôŇľeŇĄ trudno znaleŇļńá uzasadnienie dla braku gŇāadkoŇõci w obrazie izonaprńôŇľeŇĄ w Ňõrodku modelu. JednakŇľe pogŇāńôbiona analiza wskazuje na kŇāopoty algorytmu postprocesora a nie na bŇāńÖd modelu. Wskaz√≥wka d : NiemoŇľliwe jest aby w symetrycznym modelu (ksztaŇāt, podparcie, obcińÖŇľenie) uzyskane wyniki byŇāy pozbawione waloru symetrii. Jak widańá juŇľ przy pierwszych przymiarkach dostrzec moŇľna bŇāńÖd modelowania. Jednak aby znaleŇļńá na czym on polega potrzebna jest pogŇāńôbiona analiza. Aby lepiej przyjrzeńá sińô problemowi proponujńô obejrzeńá mapkńô naprńôŇľeŇĄ normalnych w kierunkach osi X i Y: 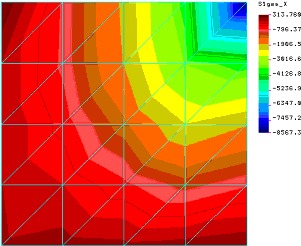 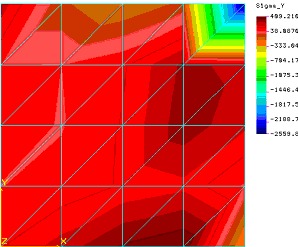
Rys.4 Chońá obraz naprńôŇľeŇĄ normalnych w kierunku osi X nie jest caŇākowicie symetryczny to dopiero naprńôŇľenia w kierunku prostopadŇāym obrazujńÖ nam caŇākowicie bŇāńôdny (wzglńôdem zaŇāoŇľeŇĄ) obraz naprńôŇľeŇĄ (zwr√≥ńámy jednak uwagńô Ňľe duŇľe gradienty powodujńÖce „skokowoŇõńá” obrazu naprńôŇľeŇĄ generowane sńÖ przez algorytm postprocesora). PoszukujńÖc Ňļr√≥deŇā niewńÖtpliwego bŇāńôdu naleŇľy wr√≥cińá do przemieszczeŇĄ. Dzieje sińô tak z dwu powod√≥w. Po pierwsze w metodzie przemieszczeniowej tylko pole przemieszczeŇĄ jest podawane w punktach wńôzŇāowych, po drugie ze wzglńôdu na nie lokalny charakter bŇāńôd√≥w (dotyczńÖ caŇāego modelu) tylko bŇāńôdy globalne mogńÖ byńá przyczynńÖ nieprawidŇāowych rezultat√≥w. UprzedŇļmy r√≥wnieŇľ pytania czytelnik√≥w - dane geometryczno fizyczne sńÖ w modelu poprawne. R√≥wnieŇľ mapy przemieszczeŇĄ w kierunku osi X i Y nie wykazujńÖ anomalii. Wygenerujmy jednak mapńô przemieszczeŇĄ rotacyjnych wok√≥Ňā osi X i Y: 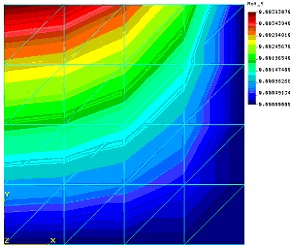 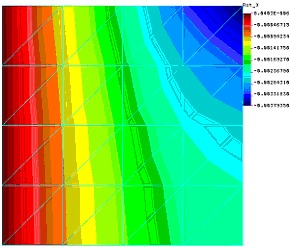
Rys 5 No i wreszcie wyszŇāo szydŇāo z worka! Ze wzglńôdu na symetrińô ustroju mapa przemieszczeŇĄ wina byńá symetryczna. Symetria podpowiada nam teŇľ od razu gdzie leŇľy bŇāńÖd! Zwr√≥ńámy uwagńô, Ňľe ustr√≥j symetryczny powinien gwarantowańá zerowanie sińô rotacji na liniach styku z odrzuconńÖ (ze wzglńôdu na symetrińô wŇāaŇõnie) czńôŇõcińÖ konstrukcji. Tak dziejńô sińô dla przemieszczeŇĄ RY na linii r√≥wnolegŇāej do osi Y, ale juŇľ nie zachodzi dla drugiej linii symetrii i dla przemieszczeŇĄ RX. Wniosek – bŇāńÖd tkwi w modelu linii symetrii i „podejrzanńÖ” jest linia r√≥wnolegŇāa do osi X. NadszedŇā czas by odsŇāonińá karty. Oto jak zamodelowano w modelu warunki brzegowe: 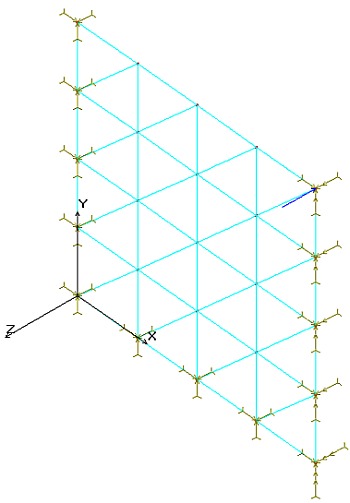
Rys 6 A jak winny byńá zamodelowane: 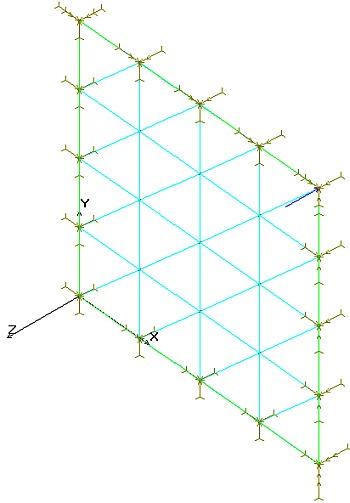
Rys 7 Podsumowanie W kolejnym artykule przybliŇľyliŇõmy nieco dwa waŇľne pojńôcia tj bŇāńôdy mierzalne i bŇāńôdy intuicyjne. Nie jest to moŇľe ŇõcisŇāy podziaŇā, jest to jednak podziaŇā naturalny – tak inŇľynier na co dzieŇĄ czuje konstrukcjńô. Widzimy juŇľ teraz, Ňľe w trakcie procesu modelowania moŇľemy popeŇānińá sporo bŇāńôd√≥w, a niestety nie wszystkie obrazujńÖ sińô w spos√≥b oczywisty. Potrzeba sporo doŇõwiadczenia i cierpliwoŇõci aby je znaleŇļńá i poprawińá. PozostaŇāa nam jeszcze do om√≥wienia walidacja i tym tematem, bodajŇľe najtrudniejszym zajmiemy sińô w trzecim artykule z serii. Na koniec pozwolńô sobie na dygresjńô. Proponujńô drodzy czytelnicy wykorzystańá ten artykuŇā w sytuacji gdy szef planuje Wam czas na obliczenia. MoŇľe chońá trochńô zyczliwszym okiem spojrzy na pozycjńô „weryfikacja modelu”. | 
