WSTДҷP Gdzie przebiega granica stosowania rГіЕјnych teorii gdzie np. jest granica pomiДҷdzy prДҷtem cienkoЕӣciennym a klasycznД… belkД…? JeЕјeli patrzymy na teoriДҷ to podstawowД… kwestiД… jest dopuszczalnoЕӣДҮ zaЕӮoЕјeЕ„ co do rozkЕӮadu naprДҷЕјeЕ„ w Еӣciankach prДҷta (patrz Rysunek 1, [ 0]i [ 0]) oraz dopuszczalnoЕӣДҮ deplanacji i deformacji przekroju. (dla prДҷtГіw cienkoЕӣciennych to uproszczona forma jednolitego rozkЕӮadu naprДҷЕјeЕ„ w pЕӮaszczu oraz branie pod uwagДҷ jedynie naprДҷЕјeЕ„ w osi wzdЕӮuЕјnej prДҷta oraz ЕӣcinajД…cych o kierunku wzdЕӮuЕјnym i poprzecznym stycznych w kaЕјdym punkcie do pЕӮaszczyzny tworzД…cej prДҷta (Rysunek 2) oraz istnienie idealnie sztywnych w swych pЕӮaszczyznach Ејeber; dla klasycznej belki to zaЕӮoЕјenie o pЕӮaskoЕӣci i niezmiennoЕӣci przekroju oraz pozostawaniu tegoЕј przekroju jako prostopadЕӮego do osi belki). 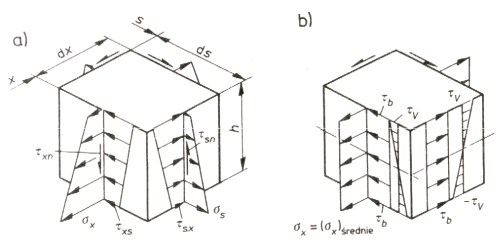
Rysunek 1 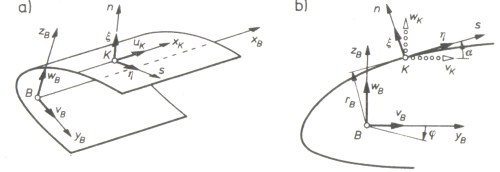
Rysunek 2 WeЕәmy do tego jeszcze uogГіlnione teorie belek np.[ 1] w ktГіrych rezygnujДҷ siДҷ z zaЕӮoЕјeЕ„ dotyczД…cych zachowania siДҷ przekroju, (pamiДҷtajД…c Ејe jej ograniczone praktyczne stosowanie wynika ze zЕӮoЕјonoЕӣci teorii). Jak wiДҷc bardziej ЕӣciЕӣle zbadaДҮ rГіЕјnicДҷ? Na ile podstawowa teoria belek moЕјe byДҮ stosowanД… wraz np ze zmianД… parametrГіw przekroju. Jednym z podejЕӣДҮ jest niewД…tpliwie analiza konstrukcji pod kД…tem stosunkГіw wymiarowych. Jednak zalecenia spotykane w literaturze sД… trudne do zastosowania zwЕӮaszcza w warunkach przejЕӣciowych bД…dЕә odbiegajД…cych od czystych postaci zgodnych z zaЕӮoЕјeniami. Trudno bowiem opieraДҮ siДҷ na stwierdzeniu, Ејe prДҷt cienkoЕӣcienny to taki w ktГіrym: „gruboЕӣДҮ pЕӮaszcza h jest wielokrotnie mniejsza od caЕӮkowitej dЕӮugoЕӣci c konturu z kolei dЕӮugoЕӣДҮ konturu c jest znacznie mniejsza od dЕӮugoЕӣci l prДҷta...” (cytat za [ 0]). Dla nas szczegГіlnie interesujД…cym bДҷdzie problem gdy warunki konstrukcyjne sД… mieszankД… konstrukcji rГіЕјnych teoretycznych modeli. Konkretnie skupmy uwagДҷ na przypadku gdy konstrukcja belki przechodzi od stanu ewidentnie pasujД…cego do klasycznej teorii do stanu, ktГіrego teoretycznД… przynaleЕјnoЕӣДҮ do teorii klasycznej, rozszerzonej czy teЕј prДҷtГіw cienkoЕӣciennych okreЕӣliДҮ jest trudno. PrzykЕӮadem technicznym sД… tu np. belki noЕӣne kЕӮadek, mostГіw stalowych (patrz, Rysunek 3), ktГіrych gГіrna powierzchnia jest jednoczeЕӣnie skonstruowana dla przenoszenia naprДҷЕјeЕ„ pochodzД…cych od obciД…ЕјeЕ„ lokalnych, pozostaЕӮe zaЕӣ Еӣciany to klasyczna, speЕӮniajД…ca wszelkie warunki konstrukcja prДҷta cienkoЕӣciennego. 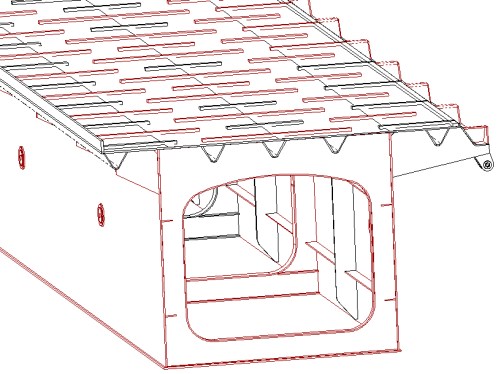
Rysunek 3
Aby przeЕӣledziДҮ zmiany jakie zachodzД… przy przechodzeniu modelu od jednego wariantu teoretycznego do drugiego wykonajmy test obliczeniowy z zastosowaniem teorii bardziej ogГіlnej od kaЕјdej teorii belek – teorii pЕӮyt i powЕӮok i to zarГіwno w wymiarze teorii powЕӮok cienkoЕӣciennych jak i gruboЕӣciennych.
Zarys teorii Podstawy teoretyczne problemu dotyczД…cego belek sД… szeroko omawiane w literaturze, Ејeby wymieniДҮ choДҮby kanon literatury dla belek klasycznych wg zaЕӮoЕјeЕ„ Bernoulliego[ 0],[ 0 czy [ 0] i nie ma potrzeby przytaczaДҮ ich w tym miejscu. NaleЕјy jednak przypomnieДҮ, Ејe skutkiem zaЕӮoЕјeЕ„ teorii klasycznej jest zerowanie siДҷ naprДҷЕјeЕ„ stycznych co prowadzi do wniosku o zerowaniu siДҷ siЕӮ poprzecznych, bo przecieЕј 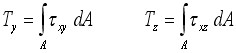 ( 1) ( 1)
gdzie: Ty,z siЕӮy poprzeczne,
A -pole przekroju poprzecznego prДҷta, τxy, τxz – naprДҷЕјenia styczne
Jest to oczywiЕӣcie sprzeczne z rГіwnaniami rГіwnowagi. Dla zachowania rГіwnaЕ„ rГіwnowagi, ktГіrych speЕӮnienie jest warunkiem bezwzglДҷdnym, stosujД…c podejЕӣcie prezentowane chociaЕјby w pracy [ 0] otrzymamy wyraЕјenie definiujД…ce naprДҷЕјenia styczne w prДҷcie zginanym siЕӮД… poprzecznД…: gdzie 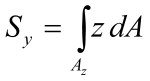 moment statyczny, moment statyczny,
pozostaЕӮe oznaczenia wyjaЕӣnia rysunek 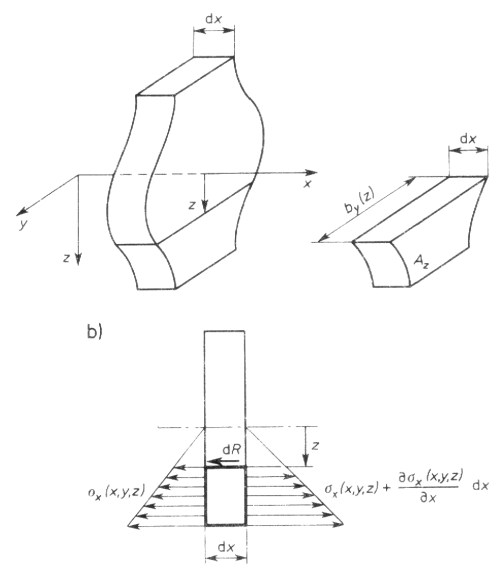
Rysunek 4 TeoriД… w oparciu o ktГіrД… bДҷdziemy weryfikowaДҮ podstawowД… teorie belek [ 0] jest teoria pЕӮyt i powЕӮok. Literatura przedmiotu jest rГіwnie bogata jak w przypadku belek tu naleЕјy wspomnieДҮ jedynie o podstawowych pozycjach [ 0],[ 0] czy teЕј [ 0] i [ 0. Uwaga ta rГіwnieЕј dotyczy teoretycznych podstaw numerycznych metod obliczeniowych teorii pЕӮyt i powЕӮok wykorzystanych w niniejszej pracy, warto tu przytoczyДҮ przede wszystkim absolutny kanon literaturowy [ 0] , w pracy korzystano rГіwnieЕј z [ 0]. Ponadto problemy te sД… szeroko omawiane w licznych publikacjach i zainteresowanych teoretycznД… stronД… odsyЕӮamy do tej literatury. ZaЕӮoЕјenia do doЕӣwiadczenia Wykonajmy szereg modeli belki podpartej przegubowo. KaЕјdy model bДҷdzie dotyczyЕӮ belki o nastДҷpujД…cych parametrach geometrycznych: DЕӮugoЕӣДҮ - 10 [m] KsztaЕӮt przekroju - skrzynkowy WysokoЕӣДҮ - 0.15 [m] Moment bezwЕӮadnoЕӣci przekroju: - 0.000010974 [m4]
Modele bДҷdД… posiadaЕӮy nastДҷpujД…ce wЕӮasnoЕӣci materiaЕӮowe: Do modeli przyЕӮoЕјono obciД…Ејenie ciД…gЕӮe: - q - 175.56 [N/m] Aby uchwyciДҮ wpЕӮyw zmian ksztaЕӮtu przekroju poszczegГіlne modele rГіЕјniД… siДҷ pomiДҷdzy sobД… tylko gruboЕӣciД… Еӣcianek bocznych (ЕӣrodnikГіw) zaЕӣ dla zachowania staЕӮej wartoЕӣci momentu bezwЕӮadnoЕӣci przekroju zmieniano szerokoЕӣДҮ przekroju D przy staЕӮej wysokoЕӣci przekroju H. 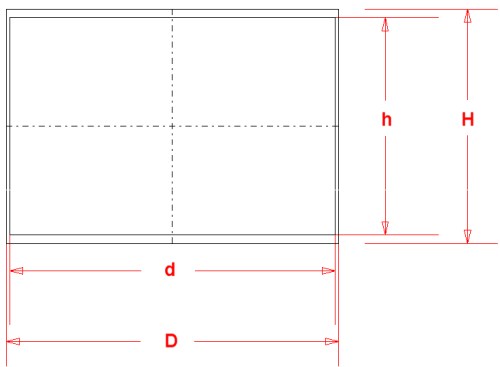
Rysunek 5
Oznaczenia wymiarГіw przekroju przedstawia Rysunek 5. Wymiary dla wykonanych modeli przedstawia tabela: | Numer modelu | D [m] | d [m] | gruboЕӣДҮ Еӣrodnika | H [m] | h [m] | I [m4] | | 1 | 0.121724 | 0.101724 | 0.02 | 0.15 | 0.14 | 0.000010974 | | 2 | 0.165210 | 0.155210 | 0.01 | 0.15 | 0.14 | 0.000010974 | | 3 | 0.186954 | 0.181954 | 0.005 | 0.15 | 0.14 | 0.000010974 | | 4 | 0.20 | 0.198 | 0.002 | 0.15 | 0.14 | 0.000010974 | | 5 | 0.204349 | 0.203349 | 0.001 | 0.15 | 0.14 | 0.000010974 | | 6 | 0.206523 | 0.206023 | 0.0005 | 0.15 | 0.14 | 0.000010974 | | 7 | 0.208262 | 0.208162 | 0.0001 | 0.15 | 0.14 | 0.000010974 | -
-
Uwagi do modelowania i obliczeЕ„ Jak powiedzieliЕӣmy wczeЕӣniej weryfikacjДҷ przeprowadzimy w oparciu o teoriДҷ pЕӮytowo-powЕӮokowД…. OczywiЕӣcie zastosowanie wprost teorii z analitycznym rozwiД…zaniem jest trudne, dlatego w niniejszej pracy posЕӮuЕјymy siДҷ przybliЕјonД… metodД… rozwiД…zania problemu brzegowego metodД… elementГіw skoЕ„czonych. MetodДҷ implementowanД… w systemie COSMOS/M [ 0]. Wykonane modele rГіЕјniД… siДҷ tylko wielkoЕӣciami wymiarowymi. Jako ukЕӮad odniesienia zastosowano wielkoЕӣci wyliczone dla przekroju Еӣrodkowego belki wg teorii podstawowej belek tzw Bernoulliego, wzbogaconej o wyliczenie naprДҷЕјeЕ„ stycznych wg wzoru ВҜurawskiego ( 0). Warto zwrГіciДҮ uwagДҷ, Ејe podstawowe naprДҷЕјenia pochodzД…ce od zginania nie zaleЕјД… wg teorii od przyjДҷtego modelu gdyЕј wszystkie posiadajД… identycznД… wartoЕӣДҮ momentu bezwЕӮadnoЕӣci. Dla poprawy dokЕӮadnoЕӣci obliczeЕ„ modeli odniesienia zastosowano zarГіwno teoriДҷ pЕӮyt grubych (tam gdzie minimalny wymiar poprzeczny pЕӮyty byЕӮ wiДҷcej niЕј 10-krotnie wiДҷkszy od jej gruboЕӣci) jak i teoriДҷ pЕӮyt cienkich (w pozostaЕӮych przypadkach). PodziaЕӮ modelu pЕӮytowo powЕӮokowego na elementy skoЕ„czone przedstawia Rysunek 6 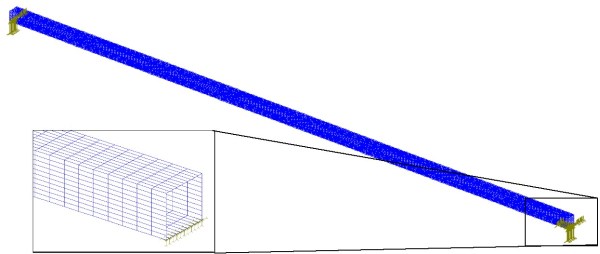
Rysunek 6 Wszystkie modele odniesienia skЕӮadajД… siДҷ z 8000 elementГіw pЕӮytowo-powЕӮokowych, czterowДҷzЕӮowych rozpiДҷtych na 8040 wДҷzЕӮach o 48185 stopniach swobody. Model pierwszy skЕӮada siДҷ caЕӮkowicie z elementГіw grubych (SHELL4T), w pozostaЕӮych, tymi elementami zamodelowano jedynie pГіЕӮkДҷ gГіrnД… i dolnД… belki, Еӣrodniki zaЕӣ zamodelowano elementami cienkimi (SHELL4). ObciД…Ејenie do modelu przyЕӮoЕјono jako siЕӮДҷ masowД….
WYNIKI Uzyskane rezultaty obliczeЕ„ przedstawia tabela. Wyniki podano z pominiДҷciem tych uzyskanych w obszarach de Saint-Venanta i specjalnie dla tych obszarГіw (*- poprawka uwzglДҷdniajД…ca obszary de Saint Venanta w modelu belkowym zmniejsza naprДҷЕјenia tnД…ce o ok. 6%). NaprДҷЕјenia redukowano wg hipotezy Hubera- Missesa.
| Model | Teoria klasyczna | Model pЕӮytowo-powЕӮokowy* | W obszarach de Saint Venanta** | | В | σx | τmax | ~max(σred) | σx | % | τmax | % | max(σred) | σx | τmax | max(σred) | | В | [Mpa] | [Mpa] | [Mpa] | [Mpa] | [Mpa] | [Mpa] | [Mpa] | [Mpa] | [Mpa] | | 1 | 14.998 | 0.372 | 14.998 | 14.853 | 0.97 | 0.343 | 7.80 | 14.862 | 14.853 | 0.587 | 14.862 | | 2 | 14.998 | 0.675 | 14.998 | 14.947 | 0.34 | 0.629 | 6.81 | 14.95 | 14.947 | 1.033 | 14.95 | | 3 | 14.998 | 1.28 | 14.998 | 15.03 | 0.21 | 1.213 | 5.23 | 14.967 | 15.03 | 2.175 | 14.967 | | 4 | 14.998 | 3.096 | 15.549 | 15.01 | 0.08 | 2.915 | 5.85 | 14.97 | 15.01 | 6.71 | 25.94 | | 5 | 14.998 | 6.121 | 17.357 | 15.13 | 0.88 | 5.782 | 5.54 | 14.98 | 15.128 | 13.005 | 49.38 | | 6 | 14.998 | 12.173 | 25.025 | 15.147 | 0.99 | 11.681 | 4.04 | 20.01 | 16.83 | 21.63 | 92.68 | | 7 | 14.998 | 60.584 | 90.56 | 15.297 | 1.99 | 22.025 | 63.65 | 39.196 | 30.06 | 40.37 | 99.57 | *- bez wynikГіw w obszarze 0.3 m od podpГіr **- dla modeli pЕӮytowo-powЕӮokowych
Zobaczmy jeszcze czy przekrГіj zachowuje zaЕӮoЕјenie o niezmiennoЕӣci ksztaЕӮtu. Uzyskane wyniki przedstawia Rysunek 7. 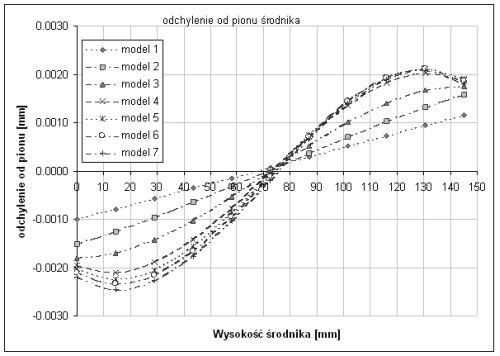
Rysunek 7 Dla uzyskania peЕӮnego obrazu przedstawmy jeszcze dla piД…tego modelu wpЕӮyw dЕӮugoЕӣci belki na wyniki naprДҷЕјeЕ„. (Obliczenia wykonano dla modelu 5 przy zaЕӮoЕјeniu staЕӮego maksymalnego momentu gnД…cego)
| DЕӮugoЕӣДҮ belki [m] | smukЕӮoЕӣДҮ | D/L | Teoria klasyczna | Model pЕӮytowo-powЕӮokowy* | W obszarach de Saint Venanta** | | | | | σx | τmax | σx | % | τmax | % | σx | τmax | | [Mpa] | [Mpa] | [Mpa] | | [Mpa] | | [Mpa] | [Mpa] | | 10 | 141 | 49 | 14.998 | 6.121 | 15.13 | 0.88 | 5.78 | 5.54 | 15.13 | 13.01 | | 5 | 71 | 24 | 14.998 | 6.121 | 15.55 | 3.68 | 11.13 | 81.82 | 45.33 | 34.33 | | 2 | 28 | 10 | 14.998 | 6.121 | 18.48 | 3.68 | 24.8 | 305.14 | 65.06 | 89.23 | | 1 | 14 | 5 | 14.998 | 6.121 | 29.01 | 93.43 | 52.05 | 750.31 | 52.06 | 211.02 | Z obliczeЕ„ wynika wyraЕәnie pojawienie siДҷ bardzo szybko odstДҷpstw od teorii. JednakЕјe jeЕјeli przyjrzymy siДҷ uwaЕјnie rozkЕӮadowi naprДҷЕјeЕ„ (Rysunek 8- dla modelu o dЕӮugoЕӣci 2 metrГіw) w modelu naprДҷЕјenia sД… wynikiem pojawienia siДҷ zjawisk ugiДҷcia poprzecznego pГіЕӮek pod wpЕӮywem obciД…Ејenia masowego. JeЕјeli by braДҮ pod uwagДҷ naprДҷЕјenia na krawДҷdziach pГіЕӮek zgodnoЕӣДҮ z teoriД… zachodzi jeszcze dla smukЕӮoЕӣci rzДҷdu 70.


Rysunek 8
Wnioski JuЕј pobieЕјna analiza uzyskanych wynikГіw wskazuje na bardzo optymistyczne wnioski. Klasyczna teoria belek daje rezultaty poprawne w znacznie szerszym zakresie niЕј naleЕјaЕӮoby siДҷ spodziewaДҮ po rozlicznych prГіbach jej udoskonalenia [ 0]. W zasadzie wyniki sД… poprawne dla szeЕӣciu z siedmiu modeli i jedynie w modelu o Еӣrodniku gruboЕӣci 0.1[mm](!) wyniki wskazujД… na kres moЕјliwoЕӣci teorii. NiezgodnoЕӣДҮ obliczeЕ„ jest poniЕјej 10% a jeЕјeli uwzglДҷdniДҮ dane bez obszarГіw de Saint Venanta (o 6% mniejsze naprДҷЕјenia tnД…ce) To zgodnoЕӣДҮ siДҷga 2%. Z technicznego punktu widzenia jest to rГіЕјnica nieistotna. Ciekawym wnioskiem pЕӮynД…cym z obliczeЕ„ jest, Ејe faЕӮszywoЕӣДҮ zaЕӮoЕјenia o niezmienniczoЕӣci przekroju (Rysunek 7) ze wzglДҷdu na niewielkД… wartoЕӣДҮ bezwzglДҷdnД… tych deformacji (<0.003 mm przy strzaЕӮce ugiДҷcia rzДҷdu 10mm) wpЕӮyw tej niezgodnoЕӣci na wyniki jest znikomy. PЕӮynie stД…d wniosek , Ејe zaЕӮoЕјenie to jest dobrym przybliЕјeniem. Ponadto warto zauwaЕјyДҮ Ејe w modelu 1 i 2 deformacja zmienia przekrГіj z prostokД…ta w trapez, dopiero dalsze modele zachowujД… siДҷ zgodnie z zaawansowanД… teoriД… belek [ 0]. I na koniec spostrzeЕјenie Ејe nawet uwzglДҷdniajД…c obszary de Saint Venanta naprДҷЕјenia redukowane obliczone wg teorii belek z uwzglДҷdnieniem poprawki na naprДҷЕјenia tnД…ce, byЕӮy w porГіwnaniu do badanych modeli co najwyЕјej wiДҷksze. Tak wiДҷc obliczenia tД… metodД… sД… bezpieczne nawet po przekroczeniu granic jej stosowania. NaleЕјy jednak zaznaczyДҮ, Ејe ostatni wniosek nie ma charakteru ogГіlnego. Dowodzi tego, znajdujД…ca peЕӮne potwierdzenie w niniejszej pracy teza z pracy [ 0], Ејe podstawowym parametrem klasyfikujД…cym rodzaj zastosowanej teorii jest smukЕӮoЕӣДҮ prДҷta. Dla belki pokazanej w niniejszej pracy teoria klasyczna traci swД… moc obowiД…zujД…cД… juЕј dla smukЕӮoЕӣci mniejszych niЕј 100. PodstawowД… przyczynД… jest duЕјy wpЕӮyw obciД…ЕјeЕ„ masowych na lokalne deformacje przekroju prДҷta (o rzД…d wielkoЕӣci wiДҷkszych niЕј w modelach 1-7), a wiДҷc nie zachowanie podstawowych zaЕӮoЕјeЕ„ klasycznej teorii (Rysunek 9- przedstawia powiДҷkszonД… deformacjДҷ przekroju prДҷta w dwu rzutach).  
Rysunek 9
BIBLIOGRAFIA
[ 0] Brzoska Z Statyka i statecznoЕӣДҮ konstrukcji prДҷtowychi cienkoЕӣciennych Warszawa PWN 1961 [ 0] MichaЕӮ ВҜyczkowski Mechanika techniczna - wytrzymaЕӮoЕӣДҮ elementГіw konstrukcyjnych Warszawa PWN 1988 [ 0] Simo, J.C., Vu-Quoc A geometrically-exact rod model incorporating shear and torsion-warping deformation, International Journal of Solids and Structures 27, 1991, 371-393 [ 0] S.Timoshenko Goodier J. Teria sprДҷЕјystoЕӣci Arkady, Warszawa 1962 [ 0] Huber M.T., Teoria sprДҷЕјystoЕӣci, PWN Warszawa 1954. [ 0] Mossakowska Z.,Nowacki W.,SokoЕӮowski M., WesoЕӮowski Z. Mecjanika techniczna t IV SprДҷЕјystoЕӣДҮ. Warszawa PWN 1978 [ 0] Zienkiewicz O.C., Taylor R.L., Thy Finite Element Method, Fourth edition, 1991. [ 0] RusiЕ„ski E., Metoda elementГіw skoЕ„czonych - system Cosmos/M, WKЕҒ Warszawa 1994. [ 0] Brzoska Z WytrzymaЕӮoЕӣДҮ materiaЕӮГіw Warszawa PWN 1972 [ 0] Nowacki W. DЕәwigarypowierzchniowe Warszawa PWN 1979 [ 0] NiezgodziЕ„ski M.E., NiezgodziЕ„ski T. WytrzymaЕӮoЕӣДҮ materiaЕӮГіw Warszawa PWN 1979
| 
