Literatura przedmiotu podaje dwa pojęcia weryfikacja i walidacja. Ten pierwszy termin odnosząc się właśnie do weryfikacji uzyskanego rozwiązania (podkreślę, że jakieś rozwiązanie musi już być) jest nam bliższy. Jednakże błędy grube, o czym warto pamiętać, to bardzo często jest też strefa walidacji. Walidacji czyli weryfikacji przyjętych założeń. I choć być może bardziej pasowałby tu termin błędy fundamentalne pozostanę przy moim oznaczeniu i zdefiniuję błędy grube jako te , które powodują generalną zmianę uzyskanych wyników. Pozostałe błędy, wedle tej klasyfikacji powodują zaś odstępstwa lokalne lub niewielkie wartościowo (licząc oczywiście względnie).
Choć błędy grube należą do wydawałoby się łatwych do znalezienie niestety tak nie jest. Podstawową przyczyną jest właśnie to, że zwykle trudny do odszukania (a nawet zorientowania się, że go popełniamy) błąd gruby powstaje u samych postaw obliczeń. Właśnie wtedy gdy tworzymy zręby naszych obliczeń: gdy dobieramy model do opisywanych zjawisk, gdy gromadzimy dane dot. modelu, gdy budujemy pierwsze szkice modelowanego zjawiska.
Co innego oczywiste błędy grube, przyłożenie siły 10-krotnie większej, zmiana stałych materiałowych o trzy rzędy wielkości, itp. Przy odrobinie intuicji wyniku zarówno zorientowanie się co do błędu jak i jego odszukanie nie powinno nastręczyć problemów. W pierwszej części artykułu nazwałem je błędami mierzalnymi, ze względu na fakt, że rozpoznajemy je po wartości uzyskanych parametrów fizykalnych: np. przemieszczeniu lub naprężeniu maksymalnym .
Aby zrozumieć błędy mierzalne najlepiej pokażę na przykładach ich wpływ na uzyskiwany wynik. Na pierwszy ogień weźmy zmiany pewnych parametrów fizycznych (stałych fizycznych i geometrycznych ) modelu. Pozwoli to na wyrobienie sobie pewnego wyczucia co do prawidłowości wyników.
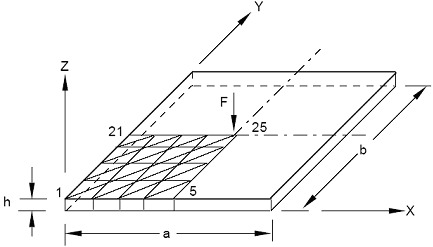
Jako przykład weźmy referencyjny model dla wielu systemów liczących. Jest to płyta prostokątna prosto podparta opisana przez Timoshenko, S. P. and Woinowsky-Krieger, “Theory of Plates and Shells,” McGraw-Hill Book Co., 2 wydanie z 1962 r. na stronach 120-143.
Płyta jest wykonana ze stali stopowej o parametrach (w celu porównania z innymi systemami liczącymi zachowałem oryginalne jednostki anglosaskie):
E = 30,000,000 psi =210000 MPa
ν= 0.3
h = 1 in = 25,4 mm
a = b = 40 in = 1012 mm
F = 400 lbf =1779,2888N
Ze względu na symetrię zamodelowano ¼ płyty, obciążenie przyłożono w jej środku (węzeł 25) Problem przedstawiono na poniższym rysunku (rys.1). Uzyskajmy w pierwszym podejściu prawidłowe wyniki.

Rys.1
O jakości rozwiązania numerycznego świadczy odstęp od rozwiązania teoretycznego, które wynosi : 0.0270230 [in] błąd wynosi więc mniej niż 0.4%.
Sprawdźmy teraz wpływ zmian własności materiałowych na wynik:
Opis modelu | Max naprężenia [psi] | Max przemieszczenie [in] |
| Referencyjne MES | 7865.2 | 0,027123 |
|
|
| |
| h= 1 in=25.mm E= 30,000,000 psi =210000 MPa ν = 0.1 zmniejszamy współczynnik poissona 3 krotnie | 6661.3(zm. 15,3%) | 0,029489(zm. 8,3%) |
|
|
| |
| h= 1 in=25.mm E=3,000,000 psi =21000 MPa ν =0.3 zmniejszamy moduł Younga 10 krotnie | 7851(zm. 0.1%) | 0, 22369(zm. 724%) |
|
|
| |
| h=0.1 in=2.53.mm E= 30,000,000 psi =210000 MPa ν = 0.3 grubość płyty zmniejszona 10 krotnie | 785110(zm.9882%) | 27.123(zm. 99900%) |
|
|
|
Zauważmy na początek, że tylko zmiana współczynnika poissona spowodowała istotniejszą zmianę jakościową obrazu pola naprężeń (choć w bardziej skomplikowanym modelu trudno tę zmianę uznać za „wykrywalną”). Dokładnie odwrotna sytuacja jest w wynikach ilościowych. Największa zmiana zaszła w modelu, który w obrazie jakościowym jest bardzo zbliżony do wyniku referencyjnego w modelu z pomyłką w grubości płyty. Co ciekawe obraz jakościowy pola przemieszczeń różni się w sposób zauważalny tylko przy zmianie modułu Younga i grubości płyty. Zmiana współczynnika poissona nie wywiera zaś istotnego wpływu.
Ciekawostką, choć oczywistą ze względu na matematyczną stronę zagadnienia, jest wpływ zmiany modułu Younga na pole naprężeń – a właściwie jego brak. Jednak często nie zastanawiamy się nad realnymi konsekwencjami zapisów równań, dlatego warto uzmysłowić sobie to na konkretnym problemie.
Jak widać na podstawie powyższych przykładów istnieje potrzeba znajomości przybliżonej wartości oczekiwanego wyniku. Bez tej wiedzy będziemy mieli kłopoty nie tyle ze znalezieniem błędu ile w zorientowaniu się, że go popełniamy. Widać też na powyższych przykładach, że jeżeli nie dysponujemy wiarygodnym benchmarkiem naszego zagadnienia, musimy szczególnie dużo uwagi poświęcić weryfikacji danych.
Podział błędów, który tu proponuje wynika z faktu, że preferuję podejście praktyka. Nie zależy mi na klasyfikacji błędów jako takich ale na usystematyzowaniu podejścia do znajdowania błędów w naszych modelach. Skąd więc nazwa błędy intuicyjne? Są to bowiem błędy, które najczęściej wyczuwamy w uzyskanych wynikach na podstawie intuicji wyrobionej doświadczeniem i dopiero tak ”wykryte” błędy staramy się zdiagnozować. Oczywiście, że weryfikację należy zawsze przeprowadzać w oparciu o dostępne metody, ale z doświadczenia też wiem, że zazwyczaj wyniki obliczeń jakkolwiek szybko by nie powstawały są i tak spóźnione i presja czasu doprowadza do rezygnacji z części zabiegów weryfikacyjnych (cokolwiek naukowcy na ten temat sądzą).
Wróćmy jednak na początek do naszego przykładu. Załóżmy, że nastąpiła pewna pomyłka w więzach. Uzyskany obraz naprężeń i przemieszczeń przedstawia poniższy rysunek:
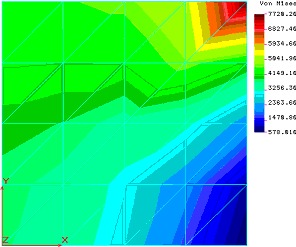
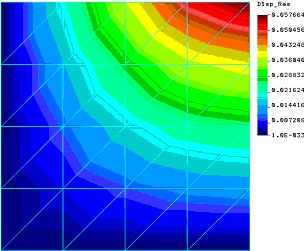
Rys.2
Na kolejnym mamy obraz deformacji płyty na tle płyty nieodkształconej, pokazano też punkt przyłożenia obciążenia:
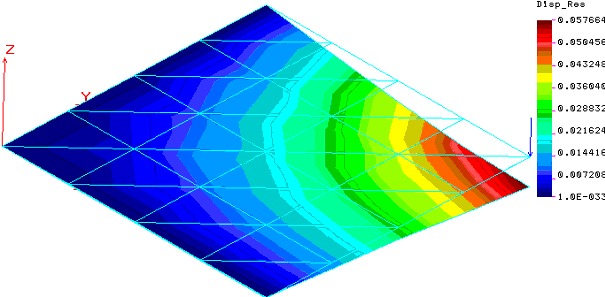
Rys 3.
Zanim zaczniemy analizę przypomnijmy sobie na co zwracać uwagę przy pierwszym kontakcie z wynikami o czym mówiliśmy w pierwszej części artykułu:
a) szukaj ekstremów (zazwyczaj jesteśmy w stanie wskazać miejsca maksymalnego i minimalnego ugięcia lub ogólnie występowania pewnej wielkości wynikowej),
b) szukaj logiki (konstrukcja „podąża” za obciążeniem),
c) szukaj „gładkości” (wszelkie duże skoki wartości wynikowych muszą mieć swój powód, bądź to w obciążeniu bądź to w charakterystyce modelu),
d) szukaj niemożliwego (np. .konstrukcja przemieszcza się w miejscu gdzie podobną są więzy).
Przeanalizujmy uzyskane wyniki pod kątem tych wskazówek:
Wskazówka a :
Obraz przemieszczeń nie budzi pod tym względem zastrzeżeń – maksima są w odpowiednim miejscu – punkt przyłożenia siły, minima także – brzeg z odebranymi stopniami translacyjnymi.
Obraz naprężeń jednak nie jest już tak poprawny. Zauważmy, żebrak powodu aby naprężenia w górnym lewym fragmencie modelu odbiegały od tych z prawego dolnego rogu. A skoro brak powodu to należy to sprawdzić!
Wskazówka b :
Konstrukcja zachowuje się logicznie odkształcenia zachodzą równomiernie w kierunku zadanego obciążenia.
Wskazówka c :
Tu w zasadzie jest tylko jeden punkt zaczepienia. W obrazie naprężeń trudno znaleźć uzasadnienie dla braku gładkości w obrazie izonaprężeń w środku modelu. Jednakże pogłębiona analiza wskazuje na kłopoty algorytmu postprocesora a nie na błąd modelu.
Wskazówka d :
Niemożliwe jest aby w symetrycznym modelu (kształt, podparcie, obciążenie) uzyskane wyniki były pozbawione waloru symetrii.
Jak widać już przy pierwszych przymiarkach dostrzec można błąd modelowania. Jednak aby znaleźć na czym on polega potrzebna jest pogłębiona analiza. Aby lepiej przyjrzeć się problemowi proponuję obejrzeć mapkę naprężeń normalnych w kierunkach osi X i Y:
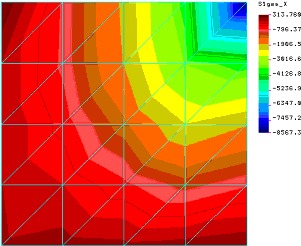
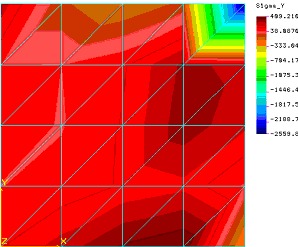
Rys.4
Choć obraz naprężeń normalnych w kierunku osi X nie jest całkowicie symetryczny to dopiero naprężenia w kierunku prostopadłym obrazują nam całkowicie błędny (względem założeń) obraz naprężeń (zwróćmy jednak uwagę że duże gradienty powodujące „skokowość” obrazu naprężeń generowane są przez algorytm postprocesora).
Poszukując źródeł niewątpliwego błędu należy wrócić do przemieszczeń. Dzieje się tak z dwu powodów. Po pierwsze w metodzie przemieszczeniowej tylko pole przemieszczeń jest podawane w punktach węzłowych, po drugie ze względu na nie lokalny charakter błędów (dotyczą całego modelu) tylko błędy globalne mogą być przyczyną nieprawidłowych rezultatów. Uprzedźmy również pytania czytelników - dane geometryczno fizyczne są w modelu poprawne. Również mapy przemieszczeń w kierunku osi X i Y nie wykazują anomalii. Wygenerujmy jednak mapę przemieszczeń rotacyjnych wokół osi X i Y:
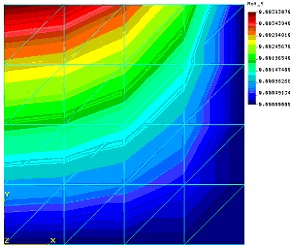
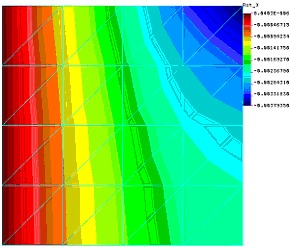
Rys 5
No i wreszcie wyszło szydło z worka! Ze względu na symetrię ustroju mapa przemieszczeń wina być symetryczna. Symetria podpowiada nam też od razu gdzie leży błąd! Zwróćmy uwagę, że ustrój symetryczny powinien gwarantować zerowanie się rotacji na liniach styku z odrzuconą (ze względu na symetrię właśnie) częścią konstrukcji. Tak dzieję się dla przemieszczeń RY na linii równoległej do osi Y, ale już nie zachodzi dla drugiej linii symetrii i dla przemieszczeń RX. Wniosek – błąd tkwi w modelu linii symetrii i „podejrzaną” jest linia równoległa do osi X.
Nadszedł czas by odsłonić karty. Oto jak zamodelowano w modelu warunki brzegowe:
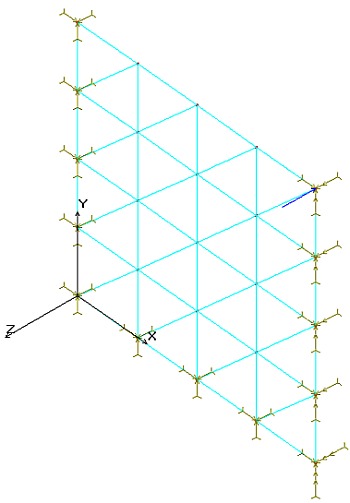
Rys 6
A jak winny być zamodelowane:
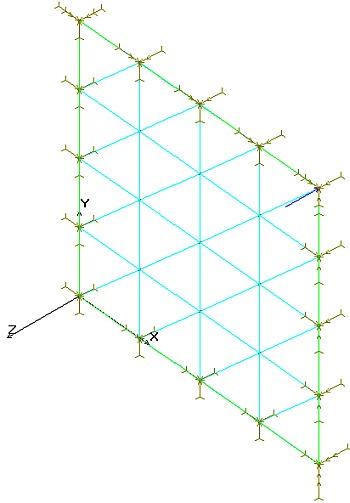
Rys 7
W kolejnym artykule przybliżyliśmy nieco dwa ważne pojęcia tj błędy mierzalne i błędy intuicyjne. Nie jest to może ścisły podział, jest to jednak podział naturalny – tak inżynier na co dzień czuje konstrukcję. Widzimy już teraz, że w trakcie procesu modelowania możemy popełnić sporo błędów, a niestety nie wszystkie obrazują się w sposób oczywisty. Potrzeba sporo doświadczenia i cierpliwości aby je znaleźć i poprawić. Pozostała nam jeszcze do omówienia walidacja i tym tematem, bodajże najtrudniejszym zajmiemy się w trzecim artykule z serii.
Na koniec pozwolę sobie na dygresję. Proponuję drodzy czytelnicy wykorzystać ten artykuł w sytuacji gdy szef planuje Wam czas na obliczenia. Może choć trochę zyczliwszym okiem spojrzy na pozycję „weryfikacja modelu”.